Musique/ Economie / Vidéo / Mathématiques

Vidéo du jour
 
 http://www.youtube.com/watch?v=KkkzTNFA4EY&feature=related

Les 5 choix musicaux du jour et le Pourquoi!

Choix 1 

 

Une oeuvre de génie méconnue

Artiste :  Pete Namlook & Bill Laswell –  Keeper of the purple twilight
http://www.youtube.com/watch?v=0BR0qKIIZbM
Si le lien ne marche pas, tapez le dans la barre d'adresse... Ce morceau de musique est incroyable.

Choix 2

 Robert Fripp n’est pas juste King Crimson!

 

Artiste :  Robert Fripp –  Bringing Down The Light
          http://www.youtube.com/watch?v=kQrTpa5nTt4

Choix 3

Un groupe qui ressemble étrangement à Pink Floyd

Extrait 1
Artiste :   Porcupine Tree Waiting  - Waiting

              http://www.youtube.com/watch?v=u8SFbyezh-U

Extrait 2    

Artiste :  Porcupine Tree Waiting  -  Waiting Phase Two
              http://www.youtube.com/watch?v=jvuZzmq6yXc&feature=related

   

Choix 4
 
Musique d’ambiance à son maximum!

While on tour in Los Angeles in 1976, O'Hearn met musician Frank Zappa, who offered him a job as bass player in his band - a position he held for over two years. During this period, O’Hearn shifted from the acoustic bass to the electric bass guitar (given the requirements of Zappa's arrangements), and also became increasingly interested in electronic music. Zappa encouraged O’Hearn to explore his premium collection of synthesizers, and also introduced him to the technical aspects of intricate physical tape editing as a way of producing 

Extrait 1
Artiste :   Patrick O'Hearn -  Beyond This Moment - theatrical trailer    

                     http://www.youtube.com/watch?v=irBU_Tra-KM&feature=related

Extrait 2    

Artiste :  Patrick O'Hearn -   So Flows The Current
                    http://www.youtube.com/watch?v=KZjAqDlEQ4c

Extrait 3    

Artiste :  Patrick O'Hearn -   Irene
                    http://www.youtube.com/watch?v=lmM1w6VR9h4

Extrait 4    

Artiste :  Patrick O'Hearn -   Magnificent River
                    http://www.youtube.com/watch?v=NUDXinDhdPE

Extrait 5    

Artiste :  Patrick O'Hearn -   Patience my friend
                    http://www.youtube.com/watch?v=IeTibl63NrY&feature=related

Choix 5

 

William Orbit, un inconnu pour vous, plus maintenant!
 
Artiste :   William Orbit -  Water From A Vine Leaf (1993)
                 http://www.youtube.com/watch?v=0Zspf6DY0vA&feature=related

      

La formule mathématique du jour

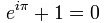
Plus belle formule mathématique

Elle est courte :

e ^ (i x π) = -1

e[puissance](i x π)[/puissance] = -1

Pas très joli sans la notation officielle mais avec les caractères standards... :|

La formule se lit "e" puissance (i fois pi) est égal à -1

Ce qui est extraordinaire est que :

e	nombre exponentiel, la base des logarithmes népériens
pi		π bon, plus connu, par exemple le rapport entre la circonférence et le diamètre d'un   cercle
i		le fameux nombre imaginaire (des nombres complexes) défini comme égal à -1 lorsqu'il est élevé au carré

Le côté surprenant est l'absence totale (connue) de rapports entre ces 3 constantes et pourtant cette formule donne un résultat "net" : aucun mathématicien au monde ne sait à ce jour expliquer pourquoi...

Leonhard Euler (Swiss mathematician and physicist, 1707-1783) and his beautiful and extraordinary formula that links the 5 fundamental constants in Mathematics, namely, e, the base of the natural logarithms, i, the square root of -1, Pi, the ratio of the circumference of a circle to its diameter, 1 and 0, together!

Euler's Equation

Euler's formula is a mathematical formula in complex analysis that shows a deep relationship between the trigonometric functions and the complex exponential function.

Euler's formula states that, for any real number x:

where

• e is the base of the natural logarithm
• i is the imaginary unit
• sin and cos are trigonometric functions.

Euler's equation or identity is a special case of the Euler' formula, where:

• 

Nous faisons aujourd'hui des choses qui auront des conséquences dans le futur, explique M. Arrow, en entrevue depuis la Californie. Le CO2 responsable de l'effet de serre restera 100, 150 ans dans l'atmosphère. Les déchets nucléaires seront dangereux pendant 10 000 ans. Nous tirons aujourd'hui des bénéfices de la production de CO2 et de déchets nucléaires, mais quelqu'un pourrait en souffrir plus tard. La question qui m'intéresse est: quel poids accorder à ces intérêts divergents?

                                                                              Kenneth Arrow

La croyance forte ne prouve que sa force, non la vérité de ce qu'on croit.

                                                                                        Nietzche

Social media ¨makes it easier for activists to express themselves,¨ he wrote, ¨and harder

 for that expression to have any impact.¨

                                                                                             Gladwell

 Imagine how our world would be different if Americans put the time they spent watching television -- an estimated 158 hours per person per month -- to productive use. This is no fantasy: Thanks to the collaborative magic of the web

                                                                                         Clay Shirky

Ensuite, le jury des Nobel d'économie, ou plus précisément le comité de 5 personnes qui propose des choix à l'Académie suédoise, n'a pas la tâche facile. Dans les vingt premières années, il a primé beaucoup de « monstres sacrés » aux larges compétences et au renom incontestable, même si leurs thèses sont remises en cause, comme Paul Samuelson (1970), John Hicks et Kenneth Arrow (1972), Friedrich Hayek (1974),  Milton Friedman (1976), James Tobin (1981) Franco Modigliani (1985), Robert Solow (1987). La plupart étaient âgés : les 53 économistes primés depuis 1969 avaient en moyenne 65 ans au moment de la remise de leur prix. L'un d'entre eux, William Vickrey, est même mort d'un infarctus en apprenant qu'il était lauréat.

 If you want to make an apple pie from scratch, you must first create the universe.

                                                                           Dr. Carl Sagan  

Demander à un économiste de prévoir avec précision le prix de l'énergie à la fin de l'année revient à demander à un spécialiste de l'évolution quelle est la prochaine espèce qui va évoluer.                   

                                                                            Kenneth Arrow

 

Article du jour : Kenneth Arrow me voici...

Un des grands économistes du vingtième siècle…

Le Monde
Economie, mercredi, 16 avril 2008, p. MDE4

ZOOM Le Monde Economie

PENSÉE ÉCONOMIQUE CHRONIQUE
Arrow et les choix collectifs

JEAN-MARC DANIEL

LES RECHERCHES des économistes sur les modes de décision collective ont parfois choisi les élections politiques comme terrain d'étude. Dès le XVIIIe siècle, Condorcet, réfléchissant sur le code électoral optimal, avait énoncé le célèbre « paradoxe de Condorcet », selon lequel une assemblée peut préférer A à B, B à C et - c'est là le paradoxe - C à A. Depuis, l'économiste qui s'est le plus illustré sur ses sujets est Kenneth Joseph Arrow.

Il naît le 23 août 1921 à New York. Après des études en mathématiques et en sciences sociales, il est officier météorologue au sein de l'US Air Force pendant la guerre du Pacifique. Cette période consolide son intérêt pour les probabilités et le décide à devenir économiste. Il enseigne à l'université Stanford de 1949 à 1968, à Harvard de 1968 à 1979, puis de nouveau à Standford.

Ses premiers travaux portent sur les élections et ce qu'il appelle le « théorème des impossibilités ». Libéral au sens politique et économique du terme, il est néanmoins amené à souligner les limites de la démocratie. Dans une société complexe, il est impossible d'obtenir une décision collective rapide et compréhensible. Il faut pour y parvenir accepter la primauté de l'opinion d'un individu sur celle des autres, c'est-à-dire l'existence de ce qu'il appelle, dans un résumé provocateur, un « dictateur ».

Arrow s'intéresse ensuite à l'équilibre de marché néoclassique. Il se demande si cet équilibre se fait au niveau d'un pays, comme le dit Walras, ou si une économie nationale doit s'interpréter comme une juxtaposition d'équilibres partiels comme le soutient Marshall. En 1954, associé à Gérard Debreu, il démontre l'existence d'un équilibre général de type walrasien. C'est le « théorème Arrow-Debreu ». Leur démonstration repose sur l'hypothèse fondatrice en économie de « rationalité des agents », rationalité qui signifie qu'ils agissent selon leur strict intérêt, et sur l'idée que l'équilibre est atteint à condition que l'on généralise la concurrence. Cette reformulation des thèses de Walras vaut à Arrow le prix Nobel de 1972 qu'il partage avec John Hicks, traducteur de Walras.

Enfin, Arrow s'intéresse à la croissance. Il associe classiquement croissance et productivité. Son originalité tient aux trois facteurs d'augmentation de la productivité qu'il identifie. En effet, au progrès technique et à la formation des travailleurs, il rajoute l'expérience acquise, qu'il appelle le « learning by doing ». Concernant le progrès technique, il indique qu'il est à la fois le fondement et la conséquence de la croissance. Concrètement, une société peu développée n'innove guère tandis que les sociétés riches accumulent les découvertes.

Lors de la mise au point de ses modèles sur la croissance, il étudie de façon poussée les fonctions de production à élasticité constante de substitution (en anglais « constant elasticity of substitution », ou CES), fonctions nommées depuis fonctions CES d'Arrow. Ces fonctions décrivent les processus de production dans lesquels la taille de l'entreprise n'a aucune conséquence sur l'arbitrage entre capital et travail.

Bien que retraité, Arrow est resté très impliqué dans la vie de Stanford. Avec le temps, ses préoccupations ont pris un tour plus philosophique, se centrant de plus en plus sur la nature même de la science économique. Agacé par les prévisions et autres conseils économiques proférés par des commentateurs à qui il dénie le titre d'économistes, il rappelle : « Demander à un économiste de prévoir avec précision le prix de l'énergie à la fin de l'année revient à demander à un spécialiste de l'évolution quelle est la prochaine espèce qui va évoluer. »